Prime Factorization

Background

We've covered how to factor and we've covered prime numbers. Let's combine these two ideas:

Question

What is the prime factorization of 16? 100? 366?

Answer

 

 

Analysis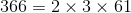

Sometimes, when working with several numbers and trying to find either a common factor or common multiple, finding the "most basic building blocks" of a given number, it's smallest factors, is helpful. We do this by finding the prime factorization of a number.

So what is that?

Let's say we're looking at the number 16. What are the factors of 16?

1, 2, 4, 8, 16

Which of those numbers is the smallest prime number? 2 (remember, 1 is not prime).

Ok - so let's state the math fact for 16 using 2 as a factor:

2 x 8 = 16

8 is composite. What's it made of? What are its factors?

1, 2, 4, 8

Which of those is the smallest prime? 2. Let's state the math fact for 8 using 2 as a factor:

2 x 4 = 8

4 is composite. Its factors are:

1, 2, 4. Let's do the math fact for 4 with 2 as a factor:

2 x 2 = 4

Ok - we've now done all these math facts. We can start putting this back together to get to the prime factorization of 16.

So we know that 2 x 8 = 16. We also know 2 x 4 = 8. So:

2 x 2 x 4 = 16

And we also know that 4 = 2 x 2:

2 x 2 x 2 x 2 = 16.

We can leave the prime factorization here, but since we also have exponentials, we can rewrite this into an exponential form:



Let's do another one. How about the number 100.

Let's do this one a slightly different way. What is a math fact for 100? Let's use 10 x 10 = 100.

10 x 10 = 100

What is a math fact for 10? 5 x 2 = 10. Notice we have two 10s, so we can substitute in for both of them:

(5 x 2) x (5 x 2) = 100

I've grouped terms to help see that we still have 10 x 10.

Ok - now we can regroup this (the associative property allows us to do this):

(2 x 2) x (5 x 5) = 100

and now let's put this into exponential form:



And now for our last one: 366. This is a big number and might be hard to do. So let's do it step by step. Let's first notice that this is an even number so we know that 2 is a factor:

2 x 183 = 366

183 is also a big number. Is it composite or prime? Turns out it's composite - it's divisible by 3:

2 x 3 x 61 = 366

61 is prime. And so the prime factorization of 366 is 2 x 3 x 61.

Vocabulary used:

• Factor - A counting number, when multiplied by another counting number, reaches a product. For instance, the factors of 6 are 1, 6, 2, and 3 (1 x 6 = 2 x 3 = 6)
• Prime Number - a counting number that has as its only factors 1 and itself. For instance, 3 is prime in that its only factors are 1 and 3. 
• Composite Number - a counting number that has more factors than 1 and itself. For instance, 4 is composite because it has as factors 1, 2, and 4. 
• Associative Property - the property that says a x (b x c) = (a x b) x c
• Base - When working with an exponential, the base is the number being multiplied. 
• Exponential - When working with an exponential, the exponential is the number of times we multiply the base.

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Prime and Composite Numbers

Operations:

• Exponentials

Associated Operations:

• Factors and Factoring

Where might we go?

Operations with different kinds of numbers:

• Addition, Subtraction, and Rational Numbers