When we do a number of identical additions, we can use multiplication to make it quicker and easier (for instance, we can say 10 x 10 = 100 instead of having to add 10 to itself ten times: 10 + 10 + 10 + ... + 10 = 100). Is there a way to do that with multiplication? Answer - yes there is...
Question
Answer
Analysis
As we started to talk about in the Background to this question, multiplication was created in order to make repeated identical additions simple to perform. Well, it's also the case that there are times when we have multiple identical multiplications to do and having a simple and easy way to notate that would help greatly in consolidating equations into easy to read forms.
Take our question for a moment. We have a 5 and we're multiplying it four times. We could simply write it as 5 x 5 x 5 x 5, but that could get awkward if we have a large number of times we're going to multiply the 5 (imagine if we had to do it twenty times!).
And so we have a way of writing this type of calculation called the exponential that helps condense the statement to something easier to read and deal with.
The number that we are multiplying is called the base. In our question, that's the 5. The number of times we're multiplying that number is called the exponent. In our question we're multiplying the 5 four times, so the exponent is 4.
We write this by first writing the base as we would any other number. We write the exponent to the upper right of the base, like this:

In our question, therefore, we write the calculation as

Another way to write it is to use the "carrot" character:
5 ^ 4
In the Order of Operations, we do exponentials after we do parentheses and before multiplication and division.
There is one rule that I should mention that might come as a surprise (I'll how why this rule is in place in a later entry) - what happens when we take a base and have 0 as the exponent? You get 1. That's right:
anything ^ 0 = 1
This includes doing this:
0 ^ 0 = 1
Weird, right?
There are a couple more rules to cover here - and these only apply when the bases are the same!
When we multiply exponentials together, say like

if we expand this out, this is what we're doing:
(5 x 5) x (5 x 5 x 5)
See that? And if we get rid of the brackets (which we can do because it's all just multiplication and the associative property says we can do this for multiplication):
5 x 5 x 5 x 5 x 5
So we have 5 and we're multiplying it 5 times. 5 is the base and because we're multiplying it 5 times, 5 is also the exponent, and so we get:

And so when we multiply exponentials with the same base, we add the exponents together:

When we take an exponential to a power, say like this:

what we're saying is that we're going to take
 and multiply itself 3 times:
and multiply itself 3 times:
Remember that

and so what we get is:
(5 x 5) x (5 x 5) x (5 x 5)
We can get rid of the brackets and now we can see that we have a base of 5 and an exponent of 6:

And so when we take an exponential to a different power, we multiply the exponents together:

Some words that you might see in a word problem that tells us we need to use an exponential:
- (Some number) to the power of... - that (some number) is the base and the exponent is the power
- (Some number) squared - we're using an exponent of 2
- (Some number) cubed - we're using an exponent of 3
- Associative Property - states that a x (b x c) = (a x b) x c
Where might you have come from?
Fact-orials Index
Operations:
Relations:
Numbers:
Operations:
Operations with different kinds of numbers:
Associated Operations:



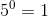
No comments:
Post a Comment
Hi there - I'm glad to see you are thinking about or maybe even getting ready to post a comment! I moderate all comments so please be patient while I hit the "ok" button on yours. Feel free to make suggestions on web resources to add, directions the entries should go,... whatever. And thanks again for leaving some feedback!