With the introduction of fractions and decimals, we now have ways of expressing the same value in the form of a fraction or in the form of a string of digits...
Question
- Express 0.25 as a fraction
- Express
 as a decimal
as a decimal - Express
 as a decimal
as a decimal - Express 4.125 as a mixed number and a fraction
- Express
 as a fraction
as a fraction - Express
 as a decimal and as a mixed number
as a decimal and as a mixed number - Express
 as an improper fraction and as a decimal
as an improper fraction and as a decimal
Analysis
As the number of operations and techniques grows, so too does our ability to use different forms to express numbers. We can express fractions and decimals and express certain kinds of decimals as fractions (more on that when we talk about Irrational Numbers). And fractions themselves can have the numerator smaller than the denominator (i.e. the top number smaller than the bottom one) and the other way around, which is called an Improper Fraction (the numerator is greater than the denominator).
The link below to the calculator soup site is a great resource - it'll automatically convert numbers from one form to another and do so with explanations.
Let's explore some of these ideas.
Question 1
0.25 as a fraction.
Let's remember that I can take any number at all and divide by 1 and not change the value of the number. That looks like this:

I can also multiply any number at all by 1 and still end up with the same number. That looks like this:

Now we get to the part that's the trick. What we'd like to see in the numerator is an integer and not a decimal. To get there, we need to multiply the numerator by 100 (0.25 x 100 = 25). We can do that, but we can't just pull a 100 out of nowhere. However, we can do it this way:

We can do this because anything (say like 100) divided by itself equals 1. So we've substituted the fraction in for 1 - this is perfectly legit!
We can now do the multiplication. The way multiplication works with fractions is that we have numerator times numerator and denominator times denominator:

Now let's factor the 100 and the 25. We can use one particular factor fact for each to help advance our problem:

Let's use the fact again that when we multiply fractions, we have numerator times numerator and denominator times denominator. And so we can do this and it's the same thing:

Remember that anything divided by itself equals 1:

And lastly, 1 times anything equals that thing:

Therefore,

Question 2
We're going the other way this time, taking a fraction and turning it into a decimal. There are a couple of ways to do this - one is to simply divide 2 by 5 (can be done on any calculator) and get 0.4.
Another way is to see that if we can put a multiple of 10 into the denominator, the numerator will tell us the decimal. Like this:

Question 3
If we put 1 divided by 9 into a calculator, we get 0.11111111 - the 1 repeats forever. There are an infinite number of fractions that when divided out into decimal form, we get a repeating decimal.
Let's look at how it happens by doing the long division:

9 is much bigger than 1, so what we need to do is to add a decimal so that we can divide 9 into a bigger number. The decimal we add is 0: 1 and 1.0 is exactly the same. We get:

9 goes into 10 once and we'll have a remainder of 1 to carry over to the next 0 decimal:

Now we have 9 dividing into 10 again... which is 1 with a remainder of 1 that carries over to the next 0... and so on...

We can show that a decimal repeats in a couple of different ways (this is more of a geographic thing). Some parts of the world use a line over the decimals that repeat. In this case we only have a 1 that is repeating, so we can say:

Other parts of the world use a dot - a single dot for a single digit. If there is a series of digits that are repeating, such as the decimal 0.123123123..., a dot is used to show the first digit repeating and another dot for the last digit. So in both bar and dot formats, this would be:

Question 4
We have 4.125 and we'll put it into mixed number and improper forms. Let's do mixed number first.
We don't need to do anything with the 4, so what we'll focus on is the 0.125. What fraction does that make?
There are a couple of ways to work it out. One way is to start with a fraction/decimal relation that we already know and use that to find this new one. For instance, we already worked out, in Question 1, that
 . If you notice, 0.125 is exactly half of 0.25, and so the fraction will be half as big as well:
. If you notice, 0.125 is exactly half of 0.25, and so the fraction will be half as big as well:
Another way to work this out is to see that with 0.125, we can rewrite it as:

We can then simplify the fraction down by taking out various forms of the number 1:
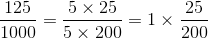

(You can do all that in a single step if you saw that 1000 is evenly divisible by 125! I did it in two steps because I think it's easier to see the process that way...)
And so as a mixed number:

So now let's make this an improper fraction (have the numerator be bigger than the denominator). To do that, let's first see that we can rewrite our mixed number:

Remember that we can add fractions together (and that whole number 4 can be expressed as a fraction because it can be divided by 1) by making sure the denominators are the same. We do that by using a clever form of 1:



and so we can say:

Question 5
We can find the value of any decimal that repeats infinitely by using this method (it's going to involve a bit of algebra, which hasn't been covered yet as an entry, so some things at this point will have to be taken on faith - we'll fix that with later entries!):
First, let's write the repeating decimal:

To make things a bit more clear, I'm going to say that "our fraction" is equal to this. And to help make that less wordy, I'll say that f, for "our fraction", is equal to this decimal:

Ok - now for the algebra trick part. What would be great is if we could just get rid of the repeating decimal and work with something that doesn't repeat. What we can do is multiply that first expression by 100 on both sides - that will move the decimal over two places and take one full recurring bit and have it on the other side of the decimal. Like this:

See that? If I have 100 of the f and add them up, I'd get 45.45 (with the repeating decimal).
And now for the next part of the trick - if I subtract the first expression from the second expression, I'll get this:

This still works - if I add up 99 of the 0.45 repeating, I get 45! (Don't try actually doing the math - the infinite carryovers will be terrible to work out!)
Ok - now I can work out what our fraction is:

Therefore,

Question 6
We're starting with an improper fraction and converting a mixed number and a decimal. Let's do the mixed number first.
We have
 . One way we can handle this kind of question is to change it into an addition statement:
. One way we can handle this kind of question is to change it into an addition statement:
I chose 16 very specifically - I know it's a multiple of 8.
Ok - we can rewrite this to show it as two fractions being added to each other:

And now we can work the divisions separately:

And we can go one step further by knowing that the one-half is the same as the decimal 0.5:

Question 7
I deliberately am ending this series of questions with a fraction with a denominator of 7. Seven, quite simply, makes messy decimals. I can't tell you why - it just does.
Ok, we have
 and we're going to turn this into an improper fraction and also a decimal.
and we're going to turn this into an improper fraction and also a decimal.Let's do the fraction first. We already know that we'll end up multiplying the 3 by the 7 - this will give us the ability to add the whole number and the fraction together. I'll run through that here:

Ok, now for the decimal. While I could run through the long division, I'd far rather reach for a calculator. The result is:

Vocabulary used:
For more information check out these links (comment to add your favourite link):
https://www.calculatorsoup.com/calculators/math/decimal-to-fraction-calculator.php
Where might you have come from?
Fact-orials Index
Numbers:
Operations with different kinds of numbers:
Associated Operations:
Relations:
Where might we go?
Operations with different kinds of numbers:


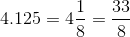

Typo: they -> the
ReplyDelete"We can now do the multiplication. They way multiplication works with fractions is that we have numerator times numerator and..."
Math error here:
"We can then simplify the fraction down by taking out various forms of the number 1:"
125/1000 = (25 * 5)/(25 * 200)
should actually be--I'm using parentheses to better format the fractions
125/1000 = (25 * 5)/(5 * 200)
Suggestion: maybe you could actually show the calculation here, especially since the algebra skills haven't been covered yet
"And now for the next part of the trick - if I subtract the first expression from the second expression, I'll get this:"
100f - f = 45.rep(45) - 0.rep(45)
99f = 45