We've talked about rational numbers, so how do we work with them and combine them? Unlike whole numbers and integers where we covered addition first and multiplication second, we'll reverse order and do multiplication first (the reason, I hope, will become clear as we go through the entries)...
Question
Evaluate:
Answer
Analysis
Question 1
Before we go diving into fractions and decimals, I want to first show operations we already know using numbers we know. But I want do the math in a more "rational number" kind of way.
Let's look at 4 x 2. One way we can look at this is by our usual multiplication process using integers:
4 x 2 = 8
Now let's remember that we can divide any number by 1 and not change the value:

We know the answer has to be 8. The way to show 8 using fractions is this way:

This example shows how we multiply fractions. If we say the numbers in the numerators and denominators can be any integers, and we can represent them by using the letters a, b, c, and d - we can say the rule for multiplying fractions is:

(keep in mind that we can't have b, d or b x d = 0! Fractions stop working when we have a denominator that's equal to 0).
What if we do the same kind of thing for dividing fractions. Let's set it up:

We can say that:

Another way to do this is to multiply by the reciprocal of the divisor - and if I explain it by getting the big words out of the way, we can take the second fraction, flip it upside down (which is the reciprocal), then multiply:

And in general:

and

Before moving on, let's talk about the answers.
When I have 4 cookies and I multiply by 2, what I'm saying is that I'm going to take those 4 cookies and I want 2 groups of them. 2 groups of 4 cookies each is 8 cookies.
When I have 4 cookies and I divide by 2, what I'm saying is that I'm going to take those 4 cookies and put them into 2 equal groups. Each group then has 2 cookies.
Question 2
We can use our rules above to find our answers here:

and

Before moving on, let's talk about the answers.
When I have 4 cookies and I multiply by a fraction, such as one half, what I'm saying is that I'm going to take those 4 cookies and I want a one-half group of them (which is the same thing as dividing by 2). And so we end up with 2 cookies.
When I have 4 cookies and I divide by a fraction, such as one half, what I'm saying is that the 4 cookies are only a part of a larger group. We divide by the fraction to find out how big the larger group is. In this case, our larger group is twice as big, and so there are 8 cookies in the larger group.
Question 3
Our rules still apply!


If I have a one-fourth (also known as a "quarter") of a pizza and I only want one half of it, I'll end up with an eighth of a piece of pizza.
If I have a quarter of a pizza but it's one half of a larger piece, that larger piece was 1/2 the pizza.
Question 4
We've changed over to working with decimals and I have to admit that I never really liked how they taught how to deal with them. So I'm going to suggest something different from the way I was taught.
Let's look at 4 x 0.2. We can rewrite it as 4 x 2 / 10. Now we can do the multiplication: 4 x 2 = 8, and then move the decimal point one spot to the left to deal with the division, which gives 0.8.
The same thing can be done with 4 / 0.2 where we can rewrite it as 4 / 2 x 10. We can work the division first, so 4 / 2 = 2, and then we multiply by 10: 2 x 10 = 20.
Question 5
Let's try rewriting these problems.
0.4 is the same as 4 / 10.
0.2 is the same as 2 / 10.
And so we can rewrite this to be 4 x 2 = 8 and then divided by 100, which means we move the decimal 2 places to the left, or 0.08.
We can do the same with the division problem, except we end up with this:
4 / 2 = 2.
With the 10s, we're dividing by a 10 (from the 0.4) and we're multiplying by a 10 (from the 0.2) and so they cancel each other out.
Vocabulary used:
For more information check out these links (comment to add your favourite link):
Where might you have come from?
Fact-orials Index
Numbers:
Operations:
Operations with different kinds of numbers:
Relations:
Operations with different kinds of numbers:
- Addition, Subtraction, and Rational Numbers
- Multiplication, Division, and Rational Numbers - Practice Problems
Relations:

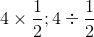








No comments:
Post a Comment
Hi there - I'm glad to see you are thinking about or maybe even getting ready to post a comment! I moderate all comments so please be patient while I hit the "ok" button on yours. Feel free to make suggestions on web resources to add, directions the entries should go,... whatever. And thanks again for leaving some feedback!