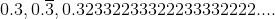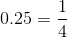Real Numbers

Background

We've talked about rational numbers, which are numbers that we can make using fractions of integers (the denominator being non-zero), which also means they can be made by terminating or repeating decimals. We've also talked about irrational numbers, which are numbers that can't be made using fractions of integers, which also means they are made by decimals that neither terminate or repeat. The two types of numbers together constitute the Real Numbers.

Question

What are some examples of Real Numbers?

Answer

All the numbers on the number line are real numbers, such as 

Analysis

Let's first look at the number line between the integers 0 and 1:



Note that between 0 and 1, there are an infinite number of numbers and of those, there are two kinds of numbers: rational and irrational.

For instance, there is 0.3, which is a terminating decimal (the red dot):



There is also the repeating decimal  (the blue dot):



Between those two points, there are irrational numbers such as 0.32332233322233332222.... (purple dot):



No matter what the decimal is, we can find it along the number line. If we graph a point for each rational and irrational, we end up with a solid line:



and, in fact, we can then look at all the rational and irrational numbers between all of the integers - and so we end up with a solid line that runs forever to the left (bigger and bigger negative numbers) and also to the right (bigger and bigger positive numbers)(I'm showing the numbers from -100 to 100 in the graph below, but the graph continues on forever in both directions):



Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Rational Numbers
• Irrational Numbers

Graphing:

• Number Line

Where might we go?

Numbers:

• Scientific Notation
• Variables 

Associated Operations:

• Estimation and Rounding 

Irrational Numbers

Background

You might have noticed, when talking about Rational Numbers, that when we dealt with decimals, we only dealt with those that either ended (the technical term is terminated), like , or repeated, like  . So what about decimals that neither terminate or repeat?

Question

What is an irrational number? How many of them sit between 0 and 1? 

Answer

The definition of an irrational number is one of exclusion (in other words, an irrational number is defined by what it isn't rather than what it is). An irrational number is neither rational (that is, can be made be made by a fraction of integers with the denominator being non-zero) nor is it imaginary (we'll talk about what this is in a later entry).

There are an infinite number of irrational numbers between 0 and 1. 

Analysis

We alluded to what an irrational number is in the Background, but let's go over what it is and isn't in more detail here.

Let's take a look at , and specifically the decimal, 0.25. We can express this terminating decimal as a fraction:



And we can go through a process with a repeating decimal to turn it into a fraction:


   

we subtract them to get:





But with an irrational number, we can't simply put a terminated decimal over an appropriate power of 10 (like 100 which is what we used for 0.25) nor can we go through a process to subtract out the repeating decimal like we did with . An irrational number has a decimal that doesn't repeat or terminate, like:

0.123456789101112131415...

The decimals can be random, or there can be a pattern that doesn't repeat (like writing out the natural numbers in order like above).

Notice that we can replace the first 1 in the series with any of the infinite number of natural numbers, and that is simply the first digit (we could do that with any digit!). Therefore, we can say that there are an infinite number of irrational numbers between 0 and 1.

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Rational Numbers

Where might we go?

Numbers:

• Pi
• Real Numbers

Addition, Subtraction, and Rational Numbers - Practice Problems

Background

Let's work some problems involving addition of rational numbers!

Question

Evaluate the following:

1.  
2.  

Answer

1. 
2. 

Analysis

Question 1

The first thing we need to do is get common denominators. I'll do that by first doing prime factorizations of the denominators:

6 = 2 x 3
3 = 3
10 = 2 x 5

Now we look at each prime number and grab the biggest group of each.

There's a single 2, a single 3, and a single 5, which means the lowest common denominator is:

2 x 3 x 5 = 30

Now let's get our fractions set up so we can do the math:







Now we want our answer in "lowest terms" - which means we're going to look if we can take out any forms of 1 that are lurking in that fraction. And there are:





Therefore:



Question 2

Let's put all of the term into improper fraction terms.

We have these terms to work with:



The first term is already in fraction form so we're set here.

For the second term, we multiply the whole number by the denominator, then add that to the numerator, like this:



For the third term, we go through the process of converting a repeating decimal to a fraction:



We've split out the 8 from the repeating decimal, so now we can focus on that decimal:





Therefore:



We combine the whole number with the fraction:



Ok - we can now rewrite our original question:



Now we need a common denominator. I'll do the prime factorizations of the denominators:

7 = 7
2 = 2
9 = 3 x 3

Ok - we need a single 2, two 3's, and a 7. That gives:

7 x 2 x 3 x 3 = 126

Let's get our fractions set up for the addition:





Let's work through to see if we need to reduce this fraction.

We know that 126 has prime factors 2, 3, and 7. If 1613 is divisible by any of these, then we'll have an opportunity to do some reducing.

Is 1613 divisible by 2? No - it's not even.
Is 1613 divisible by 3? No - the sum of its digits does not sum to a number divisible by 3.
Is 1613 divisible by 7? No - this one we can try on a calculator or we could work it through using the divisibility facts.

Therefore, the fraction can't be reduced and we can keep the answer as .

So what is this number in mixed number form and as a decimal?

As a decimal, it works out to be 12.8015873016

As a mixed number, it works out to be 

Therefore:



Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Operations with different kinds of numbers:

• Addition, Subtraction, and Integers - Practice Problems
• Addition, Subtraction, and Rational Numbers
• Multiplication, Division, and Rational Numbers - Practice Problems

Relations:

• Equality and Rational Numbers

Where might we go?

Multiplication, Division, and Rational Numbers - Practice Problems

Background

Let's work some practice problems!

Question

Evaluate:

1.  
2.  
3. 2.54 x 3.10986 x 175 

Answer

1. 
2.  
3. 2.54 x 3.10986 x 175 = 1382.33277

Analysis

Question 1

Let's see that we can rewrite the division part of the expression and turn it into a multiplication by using the inverted form of what we're dividing by:



And now we can combine the fractions:



And now we can see that we have exactly the same in the numerator and denominator, so the whole thing reduces to 1. Therefore:



It's in situations like this where we can "cancel" out terms in the numerators and denominators because they end up being a form of the number 1. Let's look at the statement again:



See the 3 in the numerator and that other 3 in the denominator? We can cancel them - we know that when we multiply the fractions together, we'll end up with 3 divided by 3, which is 1:



We cross out the 3s because with them dividing each other, they are now both 1.

And we can do the same thing with the 5s and 7s:



With all of the numerators and denominators being equal to 1, the whole thing is equal to 1.

Question 2

Let's once again notice that we have multiplication and division operations. We can convert the division operations to multiplication by taking the inverse of the fraction we are dividing by. We end up doing this:





Is there anything we can cancel? Yes - remember that 4 = 2 x 2 and that 6 = 2 x 3, so we can rewrite this way:



Now let's cancel 2s where we can:



That leaves:



Since 3, 5, and 7 are all prime, we can't do any more cancellations - we just do the multiplication and end up with the result of:



Therefore:



Question 3

I put this last question in less to work out the math (it'd be a long calculation but certainly do-able), and more to make the point that with calculators everywhere now, all we have to do is type the calculation into the machine and have it spit out the number:

2.54 x 3.10986 x 175 = 1382.33277

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Operations with different kinds of numbers:

• Multiplication, Division, and Integers - Practice Problems
• Addition, Subtraction, and Rational Numbers
• Multiplication, Division, and Rational Numbers

Relations:

• Equality and Rational Numbers

Where might we go?

Operations with different kinds of numbers:

• Addition, Subtraction, and Rational Numbers - Practice Problems