Addition, Subtraction, and Variables - Practice Problems

Background

Let's work some practice problems!

Question

Evaluate:

1. 5a + 3b + 6a - 2b 
2. 3 - 7c + 5x - 8 + 6y 

Answer

1. 5a + 3b + 6a - 2b = 7a + b
2. 3 - 7c + 5x - 8 + 6y = -5 - 7c + 5x + 6y

Analysis

When we're looking at adding and subtracting terms with variables, we combine "like terms". For instance, in Question 1, we combine the a terms and the b terms this way:

a + 3b + 6a - 2b

We can rewrite this as:

a + 6a + 3b - 2b

We can now add the terms more easily:

7a + b

Question 2

While there are a number of terms in this question, 3 - 7c + 5x - 8 + 6y, the only terms that can be worked with are the constants:

3 - 7c + 5x - 8 + 6y

3 - 8 - 7c + 5x + 6y

-5 - 7c + 5x + 6y

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Operations with Different Kinds of Numbers:

• Addition, Subtraction, and Variables

Where might we go?

Operations with Different Kinds of Numbers:

• Multiplication, Division, and Variables

Addition, Subtraction, and Variables

Background

We've covered what a variable is (it's a place holder for a number). So now let's talk about how to add them.

Question

Evaluate:

1. a + b
2. a + a
3. a - b
4. a - a

Answer

1. a + b = a + b
2. a + a = 2a
3. a - b = a - b
4. a - a = 0 

Analysis


When working with variables, we have to keep in mind that each of the variables could be a different number. For instance, in Question 1, a might equal 5 and b might equal 3. And so we can't add the two together - we have to notate that we have two separate variables. And so with the expression:

a + b

we can't do anything further with it. It is in its simplest form.

Question 2

Here we have two of the same variable, a. The variable a could be the number 6 or 3.5 or a fraction - it could be anything. Let's say for the moment it's the number 6:

a = 6

which means

a + a = 6 + 6 = 12

This is the same as doing this multiplication:

6 x 2 = 12

and so we can say this:

a + a = 2a

and to check:

6 + 6 = 2 x 6 = 12

Question 3

Just like we couldn't add a and b together in question 1, so too we can't combine them in this subtraction problem. Therefore the only thing we can say is:

a - b

Question 4

We can combine the two terms together. If we take a number (such as 6) and subtract that same number, we get 0. And so:

a - a = 0

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Operations:

• Addition
• Subtraction
• Multiplication
• Division
• Variables

Relations:

• Inverse Relations

Where might we go?

Operations with Different Kinds of Numbers:

• Addition, Subtraction, and Variables - Practice Problems
• Multiplication, Division, and Variables

Addition, Subtraction, and Rational Numbers - Practice Problems

Background

Let's work some problems involving addition of rational numbers!

Question

Evaluate the following:

1.  
2.  

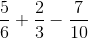
Answer

1. 
2. 

Analysis

Question 1

The first thing we need to do is get common denominators. I'll do that by first doing prime factorizations of the denominators:

6 = 2 x 3
3 = 3
10 = 2 x 5

Now we look at each prime number and grab the biggest group of each.

There's a single 2, a single 3, and a single 5, which means the lowest common denominator is:

2 x 3 x 5 = 30

Now let's get our fractions set up so we can do the math:







Now we want our answer in "lowest terms" - which means we're going to look if we can take out any forms of 1 that are lurking in that fraction. And there are:





Therefore:



Question 2

Let's put all of the term into improper fraction terms.

We have these terms to work with:



The first term is already in fraction form so we're set here.

For the second term, we multiply the whole number by the denominator, then add that to the numerator, like this:



For the third term, we go through the process of converting a repeating decimal to a fraction:



We've split out the 8 from the repeating decimal, so now we can focus on that decimal:





Therefore:



We combine the whole number with the fraction:



Ok - we can now rewrite our original question:



Now we need a common denominator. I'll do the prime factorizations of the denominators:

7 = 7
2 = 2
9 = 3 x 3

Ok - we need a single 2, two 3's, and a 7. That gives:

7 x 2 x 3 x 3 = 126

Let's get our fractions set up for the addition:





Let's work through to see if we need to reduce this fraction.

We know that 126 has prime factors 2, 3, and 7. If 1613 is divisible by any of these, then we'll have an opportunity to do some reducing.

Is 1613 divisible by 2? No - it's not even.
Is 1613 divisible by 3? No - the sum of its digits does not sum to a number divisible by 3.
Is 1613 divisible by 7? No - this one we can try on a calculator or we could work it through using the divisibility facts.

Therefore, the fraction can't be reduced and we can keep the answer as .

So what is this number in mixed number form and as a decimal?

As a decimal, it works out to be 12.8015873016

As a mixed number, it works out to be 

Therefore:



Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Operations with different kinds of numbers:

• Addition, Subtraction, and Integers - Practice Problems
• Addition, Subtraction, and Rational Numbers
• Multiplication, Division, and Rational Numbers - Practice Problems

Relations:

• Equality and Rational Numbers

Where might we go?

Addition, Subtraction, and Rational Numbers

Background

We now know how to make rational numbers. Let's learn how to add and subtract them:

Question

Evaluate:

1.   
2.  
3. 0.25 + 0.5 

Answer

1. 
2.  
3. 0.25 + 0.5 = 0.75 

Analysis

Question 1

When we're looking at adding and subtracting fractions, we can think of the operation in a couple of different ways.

One way is to think of the number line. The denominator, the 2, tells us the number of jumps we need to make to get from 0 to 1. If we're making the same number of jumps in our two fractions, then we can add up the number of jumps we've made (that's the numerator). So we can say:



Another way to view this is to think of a pizza. We take a pizza and cut it into the number of pieces in the denominator (i.e. 2). The numerator tells us the number of slices we have. And so if I have 1 out of 2 slices of pizza (that's the first fraction) and I add to it another slice of the same size, I now have an entire pizza to myself!



Question 2

When we're looking at two fractions with different denominators, we have to first make the denominators equal. Why? Well... we can answer that a couple of ways.

If we're thinking of the denominator as the size of a jump from on a number line from 0 to 1, if we're going to add the jumps together, we need to have the jumps be the same size!

If we're thinking of the denominator as the size of a piece of pizza, the two different denominators means we had two different sizes of pizza slices. We can't simply say we ate two pieces of pizza, because one was bigger and one was smaller.

When we're adding fractions, we want to add up the numerators and to do that we need the denominators to be the same. And we can do that by multiplying by clever forms of the number 1.

With our current problem, we have:



We have denominators of 2 and 3 and we'd like them to be equal. We'll find a common denominator (sometimes abbreviated as CD) and ideally the lowest common denominator (LCD). Which can get a bit confusing because this is the same as the lowest common multiple (LCM) of the denominators.

For 2 and 3, we can pretty easily see that the LCD is 6. However, let's run through a prime factorization to see it:

2 = 2 x 1
3 = 3 x 1

For the LCD, we look at each prime number and grab the biggest group of each one. For our question, there is a single 2 and a single 3. We multiply them together to get 6. So we want our denominators to each be 6. We get there by multiplying with clever forms of 1:









and so



Question 3

When we add decimals, we can put the numbers one under the next and line up the decimals (we can fill in any spots needed with 0s). In our case, we have:

0.50
0.25

and now we add down:

0.50
0.25
0.75

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Rational Numbers

Operations:

• Addition
• Subtraction

Operations with different kinds of numbers:

• Addition, Subtraction, and Integers
• Addition, Subtraction, and Integers - Practice Problems
• Multiplication, Division, and Rational Numbers

Associated Operations:

• Prime Factorization
• Multiples

Where might we go?

Operations with different kinds of numbers:

• Addition, Subtraction, and Rational Numbers - Practice Problems
• Multiplication, Division, and Rational Numbers - Practice Problems

Relations:

• Equality and Rational Numbers

Addition, Subtraction, and Integers - Practice Problems

Background

Let's work some more problems!

Question

Evaluate the following:

• -5 + (3) - (-5) + (5 - (-2))
• 4 - (3 - 4) + (-2)  
• 11 - 7 - (7 + 2)

Answer

• -5 + (3) - (-5) + (5 - (-2)) = -5 + 3 + 5 + 7 = 10
• 4 - (3 - 4) + (-2) = 4 - (-1) + (-2) = 3
• 11 - 7 - (7 + 2) = 11 - 7 - 9 = -5 

Analysis

We start with the Order of Operations. Notice that in all of the practice problems, we do have brackets to deal with. We work those first, then do the remaining math from left to right.

Question 1:

-5 + (3) - (-5) + (5 - (-2))

The brackets around the 3 are extraneous - there's no operation in there to perform, so we can simply drop them.

The brackets around the -5 are to help clarify that we are going to subtract a negative number. Brackets are often used to help readers of the expression see that there is a negative term in them. There's no operation, so again nothing to do in the first step.

The bracket set in the last term, 5 - (-2), is showing that we'll add the result of the math inside the outer set of brackets. We can do this first. 5 - (-2) = 7.

All this gives:

-5 + (3) - (-5) + (5 - (-2)) = -5 + 3 - (-5) + (7)

Now let's go ahead and simplify the - (-5) term - just like with the 5 - (-2) above, we're subtracting a negative number - which means we are, in effect, adding a positive number. And so - (-5) = +5:

-5 + 3 - (-5) + (7) = -5 + 3 + 5 + 7

And now we do the math from left to right:

-5 + 3 + 5 + 7 = -2 + 5 + 7 = 3 + 7 = 10

Question 2:

4 - (3 - 4) + (-2)

We work the bracket first:

4 - (3 - 4) + (-2) = 4 - (-1) + (-2)

And now let's work the math from left to right:

4 - (-1) + (-2) = 5 + (-2) = 3

Question 3:

11 - 7 - (7 + 2)

Again, we work the brackets first:

11 - 7 - (7 + 2) = 11 - 7 - (9)

And now we work left to right:

11 - 7 - 9 = 4 - 9 = -5

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Operations:

• Order of Operations (PEDMAS)

Operations with different kinds of numbers:

• Addition, Subtraction, and Whole Numbers - Practice Problems
• Addition, Subtraction, and Integers

Where might we go?

Operations with different kinds of numbers:

• Addition, Subtraction, and Rational Numbers
• Addition, Subtraction, and Rational Numbers - Practice Problems

Multiplication, Division, and Whole Numbers

Background

We've got Multiplication, Division, and Whole Numbers, so now let's work a problem (there are more in the Practice Problem section).

Question

Find 

Answer

Analysis

Let's first approach this using the Order of Operations. Note that the numerator (top set of terms in the fraction) and the denominator (bottom set of terms in the fraction) act as large brackets, so we don't do the division until we work the operations on the top and bottom.

Let's work the numerator first. Note that there's a bracket (coloured in red), so we work that first:

(4 + 2) x 8

(6) x 8

and now we can work the multiplication:

6 x 8 = 48

Now let's work the denominator. I'll colour the bracket again:

4 x (5 + 7)

4 x (12)

and now we can work the multiplication:

4 x 12 = 48

And now we can work the division:



Vocabulary used:

• Whole Numbers - The set of numbers that start at 0 and increase by 1 (0, 1, 2, 3,...)

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Whole Numbers

Operations:

• Multiplication
• Division
• Order of Operations (PEDMAS)

Operations with different kinds of numbers:

• Addition, Subtraction, and Whole Numbers
• Addition, Subtraction, and Whole Numbers - Practice Problems

Where might we go?

Numbers:

• Fractions and Decimals

Operations with different kinds of numbers:

• Multiplication, Division, and Whole Numbers - Practice Problems
• Multiplication, Division, and Integers

Addition, Subtraction, and Integers

Background

We've covered how to add and subtract positive numbers. With the inclusion of negative numbers, we now have to learn how to add and subtract them.

Question

Evaluate the following:

• 3 + 4
• 3 + 2
• 3 - 4
• 3 - 2
• 3 + (-4)
• 3 + (-2)
• 3 - (-4)
• 3 - (-2)
• -3 + 4
• -3 + 2
• -3 - 4
• -3 - 2
• -3 + (-4) 
• -3 + (-2)
• -3 - (-4)
• -3 - (-2) 

Answer

• 3 + 4 = 7
• 3 + 2 = 5
• 3 - 4 = -1
• 3 - 2 = 1
• 3 + (-4) = -1
• 3 + (-2) = 1
• 3 - (-4) = 7
• 3 - (-2) = 5
• -3 + 4 = 1
• -3 + 2 = -1
• -3 - 4 = -7
• -3 - 2 = -5
• -3 + (-4) = -7
• -3 + (-2) = -5
• -3 - (-4) = 1
• -3 - (-2) = -1 

Analysis

One of the trickiest concepts students run into when learning about integers is how to add and subtract (especially since practice problems will force students to make convoluted calculations). I hope this section makes adding and subtracting integers easier.

To briefly recap, integers are whole numbers that sit on either side of the number 0. We have positive integers (2, 6, 103, etc) and negative integers (-2, -6, -103, etc). So let's add and subtract some and talk about what's going on.

To make things a bit more tangible, I'm going to use a temperature analogy for this. So imagine that you are in a room and we start off at a certain number of degrees (Fahrenheit, Celsius, or whatever units you want to use) and let's say that Hot is Positive and Cold is Negative.

We start from our initial point on the number line (that first number in the equation) and then we either add or subtract heat or cold. Let's think about this for a second - if I add heat (add a positive number), the temperature of the room will go up.

If I take away heat (subtract a positive number), the temperature of the room will go down.

Ok - now what happens if we add cold (add a negative number)? The temperature of the room will go down.

And now for the hardest one of all - if I take away cold (subtract a negative number), the temperature of the room will go up.

We can now work our questions:

Positive integer plus a positive integer (it's hot and we add more heat)

3 + 4 = 7
3 + 2 = 5



Positive integer minus a positive integer (it's hot and we take away heat)

3 - 4 = -1
3 - 2 = 1



Positive integer plus a negative integer (it's hot and we add cold)

3 + (-4) = -1
3 + (-2) = 1



Positive integer minus a negative integer (it's hot and we take away cold)

3 - (-4) = 7
3 - (-2) = 5



And we can start with a negative number and it'll work the same way:

Negative integer plus a positive integer (it's cold and we add heat)

-3 + 4 = 1
-3 + 2 = -1



Negative integer minus a positive integer (it's cold and we take away heat)

-3 - 4 = -7
-3 - 2 = -5



Negative integer plus a negative integer (it's cold and we add more cold)

-3 + (-4) = -7
-3 + (-2) = -5



Negative integer minus a negative integer (it's cold and we take away cold)

-3 - (-4) = 1
-3 - (-2) = -1



You might be thinking at this point that there is no difference between 3 - 4 = -1 and 3 + (-4) = -1, that there's no difference between subtraction and adding a negative number... and you'd be absolutely right! There is no difference! And the same goes for adding a positive number and subtracting a negative number, 3 + 4 = 7 and 3 - (-4) = 7 - they're exactly the same as well!

They are treated exactly the same. So why do we have to learn this? Because the way formulas and other expressions get written, sometimes things will look like 3 - 4 and other times they'll look like 3 + (-4), and it's important that you be able to recognize them.

Vocabulary used:

• Integers - the set of numbers that start at 0 and increase by 1 (for positive integers) and decrease by 1 (for negative integers), so (...-3, -2. -1, 0, 1, 2, 3,...)
• Whole Numbers - the set of numbers that start at 0 and increase by 1 (0, 1, 2, 3,...)

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Integers
• Addition, Subtraction, and Whole Numbers

Where might we go?

Operations with different kinds of numbers:

• Addition, Subtraction, and Integers - Practice Problems
• Multiplication, Division, and Integers
• Addition, Subtraction, and Rational Numbers

Addition, Subtraction, and Whole Numbers - Practice Problems

Background 

Let's work a couple of problems in addition and subtraction using Whole Numbers:

Question

Find 4 + 5 - 2 - 1

Find (4 + 5) - (2 - 1) 

What does 2 - 1 + 4 + 3 =  ? 

Answer

4 + 5 - 2 - 1 = 6

(4 + 5) - (2 - 1) = 8

2 - 1 + 4 + 3 =  8

Analysis 

Question 1

4 + 5 - 2 - 1

We can work this question from left to right. We first look at 4 + 5 = 9:

9 - 2 - 1

Now we look at 9 - 2 = 7:

7 - 1

And now we can find the last operation: 7 - 1 = 6

6

Question 2

(4 + 5) - (2 + 1)

Now, we know from the Order of Operations, we have to do the operations within the brackets first. We can find that 4 + 5 = 9 and 2 + 1 = 3:

9 - 3

And now we can find 9 -3 = 6

6

Question 3

2 - 1 + 4 + 3 =

We can use the equals sign to help string together several statements together that get us closer to the final answer (we'll still work left to right):

2 - 1 + 4 + 3 = 1 + 4 + 3 = 5 + 3 = 8

Vocabulary:

• Whole Numbers - the set of numbers that starts at 0 and increases by 1 (0, 1, 2, 3,...)

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orial Index

Operations:

• Order of Operations (PEMDAS)

Operations with different kinds of numbers:

• Addition, Subtraction, and Whole Numbers

Properties:

• Commutative Property
• Associative Property

Where might we go?

Operations with different kinds of numbers:

• Multiplication, Division, and Whole Numbers
• Multiplication, Division, and Whole Numbers - Practice Problems
• Addition, Subtraction, and Integers - Practice Problems

Addition, Subtraction, and Whole Numbers

Background 

Now that we have learned about Whole Numbers, Addition, and Subtraction, let's work a problem (there's more problems in the Practice Problem section)

Question 

Find 5 + 2 - 3 - 1 + 6 - 0 + 0

Answer 

9

Analysis  

In prior entries, we've worked individual calculations, say like 5 + 2, both with and without the number line. We'll do the same here but we'll start on with the leftmost term and work our way through the different operations (the plusses and minuses).

We're evaluating 5 + 2 - 3 - 1 + 6 - 0 + 0

We can start with a number line and a red dot on the number 5:



So let's colour the 5 in our expression red: 5 + 2 - 3 - 1 + 6 - 0 + 0

Our first operation is plus 2 (+ 2). We move our point two numbers to the right, to 7 (I'll show that with blue):

5 + 2 - 3 - 1 + 6 - 0 + 0



Now starting at the blue dot at 7, we subtract 3 (- 3), or move 3 spots to the left. We'll land on the 4. I'll show that with green:

5 + 2 - 3 - 1 + 6 - 0 + 0



Starting at 4, we subtract 1 more to land on 3 (I'll show that in orange):

5 + 2 - 3 - 1 + 6 - 0 + 0



Now we add 6. Starting from the 3, we'll land on 9 (shown in purple):

5 + 2 - 3 - 1 + 6 - 0 + 0



And now we're asked to first subtract 0 and then add 0. Notice that when we add or subtract 0, the dot doesn't move! And so we leave our dot at 9.

This ability, to add and subtract 0 as many times as you want to any number and not change that number's value (like what we did with the 9 - we didn't change its value at all by adding or subtracting 0), gives 0 a special name - the additive identity.

Ok - so now let's work this same problem one more time, but this time without the number line. Here we go:

5 + 2 - 3 - 1 + 6 - 0 + 0

7 - 3 - 1 + 6 - 0 + 0

4 - 1 + 6 - 0 + 0

3 + 6 - 0 + 0

9 - 0 + 0

9

We start on the left and work our way to the right.

Vocabulary:

• Whole Numbers - The set of numbers that starts with 0 and increases by 1 (0, 1, 2, 3,...)

For more information check out these links (comment to add your favourite link): 
Where might you have come from? 

Fact-orials Index

Numbers:

• The Number 0
• Whole Numbers

Operations:

• Addition
• Subtraction

Graphing:

• Number Line

Where might we go?

Operations:

• Grouping Terms, Parentheses

Operations with different kinds of numbers:

• Addition, Subtraction, and Whole Numbers - Practice Problems
• Multiplication, Division, and Whole Numbers
• Addition, Subtraction, and Integers

Properties:

• Associative Property