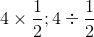Addition, Subtraction, and Rational Numbers

Background

We now know how to make rational numbers. Let's learn how to add and subtract them:

Question

Evaluate:

1.   
2.  
3. 0.25 + 0.5 

Answer

1. 
2.  
3. 0.25 + 0.5 = 0.75 

Analysis

Question 1

When we're looking at adding and subtracting fractions, we can think of the operation in a couple of different ways.

One way is to think of the number line. The denominator, the 2, tells us the number of jumps we need to make to get from 0 to 1. If we're making the same number of jumps in our two fractions, then we can add up the number of jumps we've made (that's the numerator). So we can say:



Another way to view this is to think of a pizza. We take a pizza and cut it into the number of pieces in the denominator (i.e. 2). The numerator tells us the number of slices we have. And so if I have 1 out of 2 slices of pizza (that's the first fraction) and I add to it another slice of the same size, I now have an entire pizza to myself!



Question 2

When we're looking at two fractions with different denominators, we have to first make the denominators equal. Why? Well... we can answer that a couple of ways.

If we're thinking of the denominator as the size of a jump from on a number line from 0 to 1, if we're going to add the jumps together, we need to have the jumps be the same size!

If we're thinking of the denominator as the size of a piece of pizza, the two different denominators means we had two different sizes of pizza slices. We can't simply say we ate two pieces of pizza, because one was bigger and one was smaller.

When we're adding fractions, we want to add up the numerators and to do that we need the denominators to be the same. And we can do that by multiplying by clever forms of the number 1.

With our current problem, we have:



We have denominators of 2 and 3 and we'd like them to be equal. We'll find a common denominator (sometimes abbreviated as CD) and ideally the lowest common denominator (LCD). Which can get a bit confusing because this is the same as the lowest common multiple (LCM) of the denominators.

For 2 and 3, we can pretty easily see that the LCD is 6. However, let's run through a prime factorization to see it:

2 = 2 x 1
3 = 3 x 1

For the LCD, we look at each prime number and grab the biggest group of each one. For our question, there is a single 2 and a single 3. We multiply them together to get 6. So we want our denominators to each be 6. We get there by multiplying with clever forms of 1:









and so



Question 3

When we add decimals, we can put the numbers one under the next and line up the decimals (we can fill in any spots needed with 0s). In our case, we have:

0.50
0.25

and now we add down:

0.50
0.25
0.75

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Rational Numbers

Operations:

• Addition
• Subtraction

Operations with different kinds of numbers:

• Addition, Subtraction, and Integers
• Addition, Subtraction, and Integers - Practice Problems
• Multiplication, Division, and Rational Numbers

Associated Operations:

• Prime Factorization
• Multiples

Where might we go?

Operations with different kinds of numbers:

• Addition, Subtraction, and Rational Numbers - Practice Problems
• Multiplication, Division, and Rational Numbers - Practice Problems

Relations:

• Equality and Rational Numbers

Multiplication, Division, and Rational Numbers

Background

We've talked about rational numbers, so how do we work with them and combine them? Unlike whole numbers and integers where we covered addition first and multiplication second, we'll reverse order and do multiplication first (the reason, I hope, will become clear as we go through the entries)...

Question

Evaluate:

1.  
2.  
3.  
4.  
5.  

Answer

1. 
2.  
3.  
4.  
5.  

Analysis

Question 1

Before we go diving into fractions and decimals, I want to first show operations we already know using numbers we know. But I want do the math in a more "rational number" kind of way.

Let's look at 4 x 2. One way we can look at this is by our usual multiplication process using integers:

4 x 2 = 8

Now let's remember that we can divide any number by 1 and not change the value:



We know the answer has to be 8. The way to show 8 using fractions is this way:



This example shows how we multiply fractions. If we say the numbers in the numerators and denominators can be any integers, and we can represent them by using the letters a, b, c, and d - we can say the rule for multiplying fractions is:



(keep in mind that we can't have b, d or b x d = 0! Fractions stop working when we have a denominator that's equal to 0).

What if we do the same kind of thing for dividing fractions. Let's set it up:



We can say that:



Another way to do this is to multiply by the reciprocal of the divisor - and if I explain it by getting the big words out of the way, we can take the second fraction, flip it upside down (which is the reciprocal), then multiply:



And in general:



and



Before moving on, let's talk about the answers.

When I have 4 cookies and I multiply by 2, what I'm saying is that I'm going to take those 4 cookies and I want 2 groups of them. 2 groups of 4 cookies each is 8 cookies.

When I have 4 cookies and I divide by 2, what I'm saying is that I'm going to take those 4 cookies and put them into 2 equal groups. Each group then has 2 cookies.

Question 2

We can use our rules above to find our answers here:



and



Before moving on, let's talk about the answers.

When I have 4 cookies and I multiply by a fraction, such as one half, what I'm saying is that I'm going to take those 4 cookies and I want a one-half group of them (which is the same thing as dividing by 2). And so we end up with 2 cookies.

When I have 4 cookies and I divide by a fraction, such as one half, what I'm saying is that the 4 cookies are only a part of a larger group. We divide by the fraction to find out how big the larger group is. In this case, our larger group is twice as big, and so there are 8 cookies in the larger group.

Question 3

Our rules still apply!





If I have a one-fourth (also known as a "quarter") of a pizza and I only want one half of it, I'll end up with an eighth of a piece of pizza.

If I have a quarter of a pizza but it's one half of a larger piece, that larger piece was 1/2 the pizza. 

Question 4

We've changed over to working with decimals and I have to admit that I never really liked how they taught how to deal with them. So I'm going to suggest something different from the way I was taught.

Let's look at 4 x 0.2. We can rewrite it as 4 x 2 / 10. Now we can do the multiplication: 4 x 2 = 8, and then move the decimal point one spot to the left to deal with the division, which gives 0.8.

The same thing can be done with 4 / 0.2 where we can rewrite it as 4 / 2 x 10. We can work the division first, so 4 / 2 = 2, and then we multiply by 10: 2 x 10 = 20.

Question 5

Let's try rewriting these problems.

0.4 is the same as 4 / 10.
0.2 is the same as 2 / 10.

And so we can rewrite this to be 4 x 2 = 8 and then divided by 100, which means we move the decimal 2 places to the left, or 0.08.

We can do the same with the division problem, except we end up with this:

4 / 2 = 2.

With the 10s, we're dividing by a 10 (from the 0.4) and we're multiplying by a 10 (from the 0.2) and so they cancel each other out.

Vocabulary used:

For more information check out these links (comment to add your favourite link):

Where might you have come from?

Fact-orials Index

Numbers:

• Rational Numbers

Operations:

• Multiplication
• Division

Operations with different kinds of numbers:

• Multiplication, Division, and Integers
• Multiplication, Division, and Integers - Practice Problems

Relations:

• Greater/Lesser Than and Rational Numbers

Where might we go?

Operations with different kinds of numbers:

• Addition, Subtraction, and Rational Numbers
• Multiplication, Division, and Rational Numbers - Practice Problems

Relations:

• Equality and Rational Numbers

Long Division

Background

When we have easy to divide numbers, say like , it's easy to see what the answer is (= 2). Is there a way to work out a much bigger division without using a calculator?

Question

Evaluate:

1. 
2.  using a remainder
3.  using a fractional remainder

Answer

There is a way - long division.

1.  
2.  
3.  

Analysis

While the art of long division is less important nowadays than it was before the advent of calculators, the ability to do long division will help when dividing terms that are more complicated.

So let's go over how to do this. (The link below to www.mathisfun.com has an excellent description on how to do long division.)

Let's first look at the Question 1: . Before we dive in, notice that we can also express the question as . 3836 is the numerator and 7 is the denominator.

We set up the long division by putting the numerator under a "division sign" and we put the denominator outside of that sign:



Now we're going to multiply 7 by a natural number so that we get a product bigger than the first digit of the numerator. And as we can see, there is no such number because 7 is bigger than 3.

So now what we do is do the same thing, multiply 7 by a natural number, but this time we look at the first two digits of 3836, which is 38. We want to get as close as possible but not go over. The closest we can get is 5: 7 x 5 = 35 but 7 x 6 = 42. So our quotient has as a first digit 5 (normally the line continues across over the numerator, but I can't get my equation editor to do it, so it's an over brace here):



Ok, we know 7 x 5 = 35 (we did that just above). We subtract 35 from 38 (the first two digits of the numerator) and get a difference of 3. We now make a new number for the 7 to divide into - we take the difference we just made (the 3) and take the next number of the numerator (also a 3 here) - and so we have 33 for the 7 to divide into (again, the mathisfun.com link has the more traditional look in its presentation):



We again find the largest natural number we can to multiply against the 7 so that we get as close as possible to 33 without going over. That number is 4: 7 x 4 = 28 but 7 x 5 = 35:



Our answer now has 5 and 4 in it.

4 x 7 = 28. 33 - 28 = 5 so we put the 5 in front of the 6:



Let's find the largest multiple of 7 we can make that gets as close to 56 as we can get without going over. It turns out in this case that 7 x 8 = 56 - perfect! 7 divides into 3836 evenly:



And so 3836 / 7 = 548

Question 2

Let's do something smaller to show how to work with a remainder. 

We could use the whole "dividing bar" thing and put the 3 on one side and the 16 under it. But I think we can look at this and see that 3 doesn't divide equally into 16: 3 x 5 = 15 and 3 x 6 = 18.

So our answer is 5... and something. Let's work with what that something is.

3 x 5 = 15. If we subtract 15 from 16, we have 16 - 15 = 1. What to do with that 1.

One way to deal with it is to say it's the remainder. What does that mean?

Let's think of it this way - if we have 16 freshly baked chocolate chip cookies and there are 3 people who are going to share them equally, what can we do? Each person can get 5 cookies, and so that's 15 cookies eaten. That last cookie gets put into the cookie jar for later. That last cookie is the remainder.

Question 3

So what if the three people don't want to put the cookie into the jar and instead want to share it too? Well... we can cut the cookie, can't we? There are three people, so we cut the cookie into three pieces ("thirds") and each person gets one piece each.

Each person then gets 5 whole cookies and 1 piece out of 3 pieces of that last cookie. That's 5 plus 1/3 cookies for each person. We can express this as:



Vocabulary used:

For more information check out these links (comment to add your favourite link):

https://www.mathsisfun.com/long_division.html

Where might you have come from?

Fact-orials Index

Operations:

• Division

Associated Operations:

• Dividing Evenly
• Remainders and Modulo

Where might we go?